Rovelli, capitolo 4. I quanti.

C. Rovelli, La realtà non è come ci appare, Raffaello Cortina 2014

commenti precedenti:

La scienza è fonte di valori?

Rovelli, capitolo 1
Rovelli, capitolo 2

Rovelli, capitolo 3

Riassumo (liberamente, in carattere Times; tra virgolette riporto brani del testo di Rovelli) e commento (in Helvetica).

Nel 1900 Max Planck ipotizza che l'energia (del campo elettrico) sia distribuita in quanti (unità minime, mattoncini minimi) e che l'energia di ogni quanto dipenda dalla frequenza (delle onde elettromagnetiche; in altri termini dalla velocità delle oscillazioni delle onde). Più alta è la frequenza, più grande sarà il quanto. Nel 1905 Einstein, partendo dalla spiegazione dell'effetto fotoelettrico, capisce che i quanti esistono realmente. I quanti di luce sono i fotoni: l'energia della luce è distribuita nello spazio in maniera discontinua. Questo lavoro di Einstein non viene inizialmente preso sul serio, perché ci si era appena convinti che la luce fosse un'onda del campo elettromagnetico "e come fa un'onda a essere fatta di granelli? (...) Capire come la luce possa essere sia un'onda elettromagnetica sia, allo stesso tempo, uno sciame di fotoni, richiederà l'intera costruzione della meccanica quantistica."

Nella comprensione del fenomeno della luce, quindi, si è passati dalla teoria corpuscolare (Newton) alla teoria ondulatoria (Maxwell), a una sintesi delle due teorie: la luce come onda-corpuscoli (Einstein). Non c'è, in questo procedere storico della fisica, una conferma del processo dialettico teorizzato da Hegel?

Niels Bohr, nel primo ventennio del Novecento, studiando la struttura degli atomi si imbatte in un problema. Secondo il modello dell’atomo allora condiviso (un nucleo centrale intorno a cui girano elettroni, come un piccolo sistema solare) non risultava spiegabile il fatto che la materia sia colorata. “Studiando in dettaglio la luce emessa (non sarebbe meglio dire ‘riflessa’? La maggior parte delle sostanze non sono luminose, non emettono luce propria…) dagli atomi, si ricava che le sostanze elementari hanno colori che le contraddistinguono.”

Quindi si appura che il colore è una “qualità primaria”! Avevo già commentato, a proposito del colore, nel capitolo 2, che si può interpretare la scoperta di Maxwell che le differenze di colore sono differenze di frequenza delle onde elettromagnetiche come la scoperta del lato “oggettivo” o “in sé” del colore rispetto al suo lato “soggettivo” o “fenomenico” (come noi percepiamo queste differenze di frequenza).

“Maxwell aveva scoperto che il colore è la frequenza della luce. Quindi la luce viene emessa (stessa osservazione fatta sopra…) dalle sostanze solo a certe frequenze. L’insieme delle frequenze che caratterizza una data sostanza si chiama ‘spettro’ di questa sostanza.”

“Il colore è la frequenza della luce, cioè la velocità a cui vibrano le linee di Faraday. A sua volta, questa è determinata dal vibrare delle cariche elettriche che originano la luce, e queste cariche, per la materia, sono gli elettroni che volteggiano intorno agli atomi.”  La cosa però non tornava rispetto alla meccanica newtoniana: “a credere alla meccanica di Newton, un elettrone può ruotare intorno al suo nucleo a qualunque velocità, e quindi emettere luce a qualunque frequenza. Ma allora, perché la luce emessa da un atomo non contiene tutti i colori, ma solo pochi colori particolari? Perché gli spettri atomici non sono un continuo di colori, ma sono composti da poche righe staccate?”

Bohr riesce a rispondere a questo problema, ma lo fa proponendo un nuovo modello di atomo, nel 1913, con caratteristiche che appaiono bizzarre. Ipotizza che anche l’energia degli elettroni negli atomi possa assumere solo certi valori “quantizzati” (ipotesi analoga a quella avanzata da Einstein per l’energia dei quanti di luce), che gli elettroni possano esistere solo su certe orbite, a distanze particolari dal nucleo, e che gli elettroni possano “saltare” fra l’una e l’altra delle orbite atomiche consentite (“salti quantici”). Questo nuovo modello atomico, con cui Bohr riusciva a rendere conto con precisione di tutti gli spettri di tutte le sostanze e a prevedere anche spettri non ancora osservati,  era contraddittorio rispetto alle concezioni tradizionali della materia e della dinamica. 

Sarà il giovane Werner Heisenberg ad avanzare una teoria profondamente innovativa che riusciva a inquadrare queste stranezze. Rovelli descrive molto bene le circostanze nelle quali, in una notte del 1925, nel parco dietro l’Istituto di Fisica di Copenhagen, Heisenberg ha una folgorante intuizione che lo porta a scrivere per primo le equazioni della meccanica quantistica, e lascio al lettore curioso la lettura diretta del libro di Rovelli. Qui vorrei sintetizzare e commentare l’intuizione di Heisenberg da un punto di vista filosofico. 

L’intuizione è che gli elettroni possano avere, a differenza degli oggetti materiali che siamo abituati ad osservare nelle nostre esperienze quotidiane, una esistenza intermittente! Possono scomparire e riapparire (i “salti quantici”); fra un’esistenza e l’altra non sono da nessuna parte, non hanno alcuna posizione precisa. “Gli elettroni non esistono sempre. Esistono solo quando interagiscono. Si materializzano in un luogo quando sbattono contro qualcosa d’altro. I ‘salti quantici’ da un’orbita all’altra sono il loro modo di essere reali: un elettrone è un insieme di salti da un’interazione all’altra. Quando nessuno lo disturba, un elettrone non è in alcun luogo.”

Questa esistenza intermittente avrebbe sicuramente scandalizzato Parmenide… ma proviamo a ragionarci sopra un momento. La prima questione mi sembra la seguente: esiste una modalità di esistenza, un altro modo di essere (per esempio quello che per gli stoici era il “sussistere”, che attribuivano agli enti immateriali come il significato), nella quale un elettrone si trova quando non è e che consente però di fornire una continuità all’identità dell’elettrone stesso? In altri termini: fra un salto quantico e l’altro un elettrone rimane se stesso o no? Può una cosa restare se stessa se si interrompe la continuità della sua esistenza materiale? Mi sembra che in gioco ci sia l’idea di una quantizzazione dell’esistenza stessa! 

La seconda questione è che Rovelli punta molto sull’interpretazione relazionale della teoria. Essere significherebbe interagire, relazionarsi. A questo proposito mi viene in mente che in fondo questa è la stessa idea che ha avuto Platone quando tentava di trovare un significato per l’essere che potesse funzionare sia per la sua teoria delle idee sia per l’atomismo democriteo: cosa hanno in comune le idee platoniche e gli atomi di Democrito? che possono entrare in relazione con altri enti della loro specie. Essere è essere in rapporto con. Mi sembra, però, che questa idea lasci in sospeso proprio la prima questione che ponevo sopra, cioè cosa ne è di un ente che non interagisce? Conserva la sua identità fino all’interazione successiva o no?

Altro protagonista della meccanica quantistica è Paul Adrien Maurice Dirac, gigante della fisica del XX secolo. Scrive Rovelli: "nelle sue mani la meccanica quantistica, da accozzaglia snaturata di intuizioni, mezzi calcoli, fumose discussioni metafisiche ed equazioni che funzionano bene e non si sa perché si trasforma in un'architettura perfetta: aerea, semplice e bellissima. Ma di un'astrattezza stratosferica. (...) In essa ogni oggetto è descritto da uno spazio astratto,*

*Uno spazio di Hilbert

e non ha alcuna proprietà in sé, a parte quelle che non cambiano mai, come la massa. La sua posizione e velocità, il suo momento angolare e il suo potenziale elettrico ecc. prendono realtà solamente quando si scontra con un altro oggetto. (...) L'aspetto relazionale della teoria dovente universale. (...) Non sappiamo con certezza dove l'elettrone comparirà, ma possiamo calcolare la probabilità che compaia qui o là".

Una variabile fisica può assumere solo certi valori: lo spettro di una variabile è l'insieme dei valori particolari che la variabile può assumere. Con Dirac diventa possibile calcolare quali valori possa prendere una variabile fisica: "Questo si chiama 'calcolo dello spettro di una variabile', cattura la granularità nel fondo della natura delle cose, ed è estremamente generale: vale per qualunque variabile fisica. I valori sono quelli che una variabile può prendere nel momento in cui l'oggetto (atomo, campo elettromagnetico, molecola, pendolo, sasso, stella...) (ma non vale solo su scala atomica?? Più avanti, a pag. 115, nella nota 11 Rovelli scrive: "Una regione finita dello spazio delle fasi, cioè dello spazio dei possibili stati di un sistema, contiene un numero infinito di stati classici distinguibili, ma corrisponde sempre a un numero finito di stati quantistici ortogonali. Questo numero è dato dal volume della regione diviso per la costante di Planck elevata al numero dei gradi di libertà. (???) Questo risultato è completamente generale.) interagisce con qualcos'altro (relazionalismo) (...) Cosa succeda fra un'interazione e l'altra è qualcosa che nella teoria non esiste (Un bel problema!)"

"La probabilità di trovare un elettrone, o una qualunque altra particella, in un punto o nell'altro nello spazio, si può immaginare come una nuvola diffusa, più densa dove la probabilità di vedere l'elettrone è maggiore. Talvolta è utile visualizzare questa nuvola, come fosse un oggetto reale. Per esempio, la nuvola che rappresenta un elettrone intorno al suo nucleo ci dice dove è più facile che l'elettrone appaia se proviamo a guardarlo. Se li avete incontrati a scuola, questi sono gli "orbitali" atomici.*"

(riporto qui sotto immagini degli "orbitali" atomici che si possono trovare nel web:)

"*La 'nuvola' che rappresenta i punti dello spazio dove è probabile trovare l'elettrone è descritta da un oggetto matematico chiamato la 'funzione d'onda'. Il fisico austriaco Erwin Schrödinger ha scritto un'equazione che mostra come questa funzione d'onda evolva nel tempo. Schrödinger aveva sperato che l''onda' potesse spiegare le stranezze della meccanica quantistica (...) [ma] il motivo principale per cui l'onda di Schrödinger non è una buona immagine della realtà consiste nel fatto che, quando l'elettrone collide con qualcosa d'altro, è sempre in un punto solo, non è diffuso nello spazio come un'onda. Se si pensa che un elettrone sia un'onda, ci si trova poi nella peste a cercare di spiegare come  accade che quest'onda si concentri istantaneamente in un solo punto a ogni collisione. (...) La realtà dell'elettrone non è un'onda: è questo apparire a intermittenza nelle collisioni (...)"

Per quanto strana, la teoria si rivela estremamente efficace, ed è alla base, ricorda Rovelli, dei computer, della chimica e biologia molecolare avanzate, dei laser, dei semiconduttori. Altra straordinaria applicazione della teoria è la seguente:

"prendete l'equazione della meccanica quantistica che determina la forma degli orbitali dell'elettrone. Questa equazione ha un certo numero di soluzioni e queste soluzioni corrispondono esattamente : all'idrogeno, all'elio... all'ossigeno... e agli altri elementi! La tavola periodica di Mendeleev è strutturata esattamente come le soluzioni. Le proprietà degli elementi e tutto il resto segue come soluzione di questa equazione! In altre parole, la meccanica quantistica decifra perfettamente il segreto della struttura della tavola periodica degli elementi. L'antico sogno di Pitagora e di Platone di descrivere tutte le sostanze del mondo con una sola formula è realizzato."

Dirac si rende poi conto che la meccanica quantistica si può applicare direttamente ai campi, e scopre la convergenza fra la nozione di particella e quella di campo:
"Campi e particelle sono la stessa cosa
(...)
La nuvola di probabilità che accompagna gli elettroni fra un'interazione e l'altra è un po' simile a un campo. Ma i campi di Faraday e Maxwell, a loro volta, sono fatti di grani: i fotoni. Non solo le particelle sono in un certo senso diffuse nello spazio come campi, ma anche i campi interagiscono come le particelle. (...)
Il modo in cui questo avviene nella teoria è elegante: le equazioni di Dirac determinano quali valori possa prendere ogni variabile. Applicate all'energia delle linee di Faraday, ci dicono che questa energia può prendere solo certi valori e non altri. L'energia del campo elettromagnetico può prendere solo certi valori, e quindi si comporta come un insieme di pacchetti di energia. Questi sono esattamente i quanti di energia di Planck e Einstein. Il cerchio si chiude. (...)
Le onde elettromagnetiche sono sì vibrazioni delle linee di Faraday, ma anche, a piccola scala, sciami di fotoni. Quando interagiscono con qualcosa d'altro, come nell'effetto fotoelettrico, si mostrano come sciami di particelle: sul nostro occhio la luce pioggerella in gocce separate, in singoli fotoni. I fotoni sono "i quanti" del campo elettromagnetico.
D'altra parte, anche gli elettroni e tutte le particelle di cui è fatto il mondo sono "quanti" di un campo: un "campo quantistico" simile a quello di Faraday e Maxwell, soggetto alla granularità e alla probabilità quantistiche, e Dirac scrive l'equazione del campo degli elettroni e delle altre particelle elementari.*

*L'equazione di Dirac

La differenza fra campi e particelle introdotta da Faraday viene largamente a sparire.
La forma generale della teoria quantistica compatibile con la relatività ristretta è chiamata 'teoria quantistica dei campi' ed è la base dell'odierna fisica delle particelle. Le particelle sono quanti di un campo, come i fotoni sono quanti del campo elettromagnetico, e tutti i campi mostrano questa struttura granulare nelle loro interazioni."

(le ultime due immagini sono tratte dall'articolo Il microscopio che vede gli atomi)

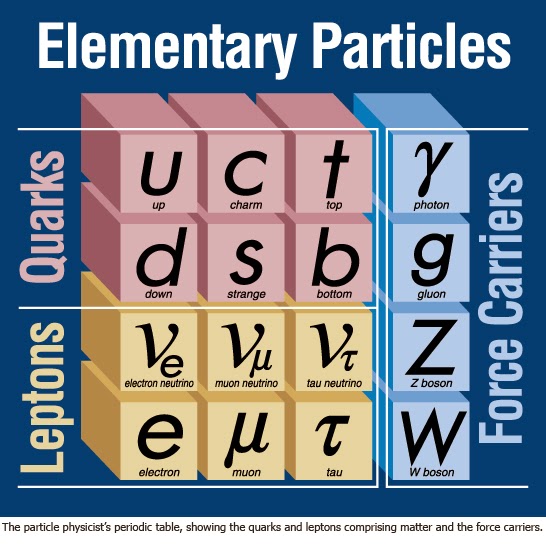
"Nel corso del XX secolo l'elenco dei campi fondamentali è stato messo a punto e oggi disponiamo di una teoria, chiamata 'modello standard delle particelle elementari', che sembra descrivere bene tutto quello che vediamo, a parte la gravità,* nell'ambito della teoria quantistica dei campi.
*. C'è un fenomeno che sembra non essere riducibile al modello standard: la cosiddetta materia oscura. Astrofisici e cosmologi osservano nell'Universo effetti di materia che sembra non essere del tipo della materia descritta dal modello standard. Ci sono molte cose che ancora non sappiamo. "

(Incredibile! Anche in questo campo, più si acquisiscono conoscenze, più si scopre quanto si è ignoranti.)

"(...) Il 'modello standard' è stato completato intorno agli anno Settanta. Ci sono una quindicina di campi le cui eccitazioni sono le particelle elementari (elettroni, quark, muori, neutrini, la particella di Higgs e poco altro), più alcuni campi, come il campo elettromagnetico, che descrivono la forza elettromagnetica e le altre forze che agiscono a scala nucleare."

Quindi ci sono, se ho capito bene, "campi-particelle" e "campi-forze".